INTRODUCCIÓN
En estadística, la regresión logística es un tipo de análisis de regresión utilizado para predecir el resultado de una variable categórica (una variable que puede adoptar un número limitado de categorías) en función de las variables independientes o predictoras. Es útil para modelar la probabilidad de un evento ocurriendo como función de otros factores (1).
LA REGRESIÓN LOGÍSTICA BINARIA
La regresión logística es usada en las ciencias médicas y sociales. Otros nombres para regresión logística usados en varias áreas de aplicación incluyen modelo logístico, modelo logit, y clasificador de máxima entropía (1).
Objetivos de la Regresión
Los modelos de regresión, como en el caso lineal, pueden usarse con dos objetivos: 1) predictivo en el que el interés del investigador es predecir lo mejor posible la variable dependiente, usando un conjunto de variables independientes y 2) estimativo en el que el interés se centra en estimar la relación de una o más variables independientes con la variable dependiente.
El segundo objetivo es el más frecuente en estudios etiológicos en los que se trata de encontrar factores determinantes de una enfermedad o un proceso.
La interacción y la confusión son dos conceptos importantes cuando se usan los modelos de regresión con el segundo objetivo, que tienen que ver con la interferencia que una o varias variables pueden realizar en la asociación entre otras.
Existe confusión cuando la asociación entre dos variables difiere significativamente según que se considere, o no, otra variable, a esta última variable se le denomina variable de confusión para la asociación. Existe interacción cuando la asociación entre dos variables varía según los diferentes niveles de otra u otras variables (2).
Asociación entre variables binomiales
Se dice que un proceso es binomial cuando sólo tiene dos posibles resultados: "éxito" y "fracaso", siendo la probabilidad de cada uno de ellos constante en una serie de repeticiones. A la variable número de éxitos en n repeticiones se le denomina variable binomial. A la variable resultado de un sólo ensayo y, por tanto, con sólo dos valores: 0 para fracaso y 1 para éxito, se le denomina binomial puntual.
Un proceso binomial está caracterizado por la probabilidad de éxito, representada por p (es el único parámetro de su función de probabilidad), la probabilidad de fracaso se representa por q y, evidentemente, ambas probabilidades están relacionadas por p+q=1. En ocasiones, se usa el cociente p/q, denominado "odds", y que indica cuánto más probable es el éxito que el fracaso, como parámetro característico de la distribución binomial aunque, evidentemente, ambas representaciones son totalmente equivalentes (3).
Los modelos de regresión logística son modelos de regresión que permiten estudiar si una variable binomial depende, o no, de otra u otras variables (no necesariamente binomiales): Si una variable binomial de parámetro p es independiente de otra variable X, se cumple p = p|X, por consiguiente, un modelo de regresión es una función de p en X que a través del coeficiente de X permite investigar la relación anterior (4).
EJEMPLO EN EL SPSS
Primero se selecciona la base de datos en la se desea trabajar, teniendo cuidado que la variable dependiente que sea motivo del análisis sea dicotómica.
Posteriormente se va al menú contextual y se selecciona ANALIZE, al cual se la un Clik.
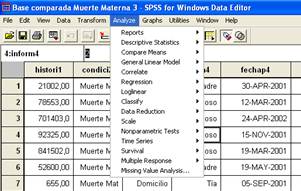
Luego se va a la sección de regresión y se selecciona binary Logistic la cual está referida a la regresión logística binaria.
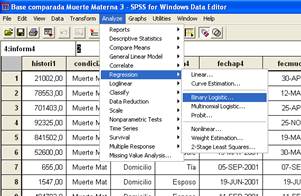
Posteriormente se ingresa en el casillero de Depndent la variable dependiente, la cual debe ser dicotómica, en este ejemplo se está tomando es de un estudio de casos y controles de mortalidad materna, la variable condición se categoriza en Muerte Materna y sobreviviente. Las variables independientes, como se ha visto con anterioridad de preferencia deben ser cuantitativa o categorizarlas de manera lógica para el análisis, para este caso y para evitar confusión emplearemos variables cuantitativas como edad, edad gestacional, peso materno, talla materna, nº de hijos vivos, intervalo íntergenésico y número de controles prenatales. Dichas variables se colocan en el casillero de covariates.
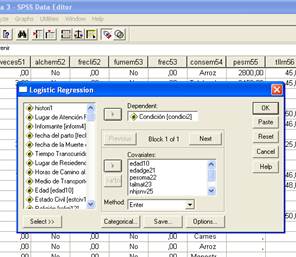
Posteriormente se reportan los resultados en el SPSS de la siguiente forma, los cuales solamente se seleccionan dos cuadros:
Logistic Regression
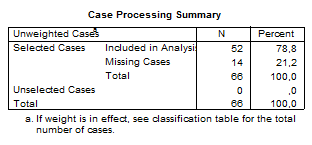

Block 0: Beginning Block
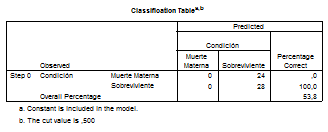
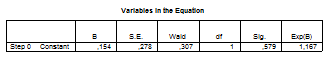
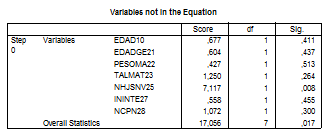
En esta tabla podemos observar que se ha calculado el valor de la significancia estadística empleándose el test de Chi² entre cada una de las variables independientes y la variable dependiente dicotómica.
Block 1: Method = Enter

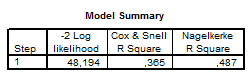
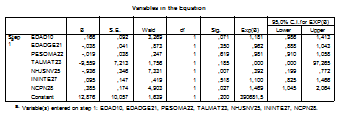
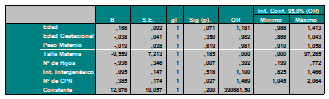
REPORTE FINAL DE REGRESIÓN LOGÍSTICA BINARIA EN SPSS Y SU INTERPRETACIÓN
Los cuadros marcados se editan en el SPSS y se escogen las pruebas de acuerdo al análisis de la información
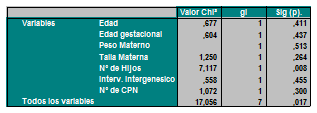
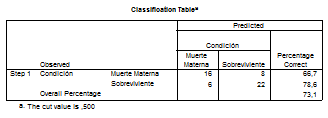
Se selecciona el segundo cuadro ya que realiza la interacción de riesgo entre las muertes maternas y las sobrevivientes, mientras que el primero solamente hace una asociación simple a la muerte materna sin comparación con las sobrevivientes.
REFERENCIAS BIBLIOGRÁFICAS
1. Hosmer D, Lemeshow S. Applied Logistic Regression (2nd edición). Wiley. ISBN 0-471-35632-8. 2000.
2. Abraira V, Pérez de Vargas A. Métodos Multivariantes en Bioestadística. Ed. Centro de Estudios Ramón Areces. 1996..
3. Silva Ayçaguer L. Excursión a la regresión logística en Ciencias de la Salud. Díaz de Santos. 1995.
4. Hosmer D, Lemeshow s. Applied Logistic Regression. John Wiley & Sons. 1989..